Computational Physical Simulations and Modeling

I am interested in developing mathematical models and scientific softwares for studying multiscale phenomena. The ultimate goal of my research is developing reduced order mathematical models based on direct (& compute-expensive) numerical simulations.

According to Holst (1994), "steps required to solve a scientific problem of current interest using modern computers [involve]:

At different stages of my career I have focused on any of these steps.

For an overview of my research work please watch my 2020 presentation (left) or my talk at ICIAM 2023 (right):

Research Highlights

- Machine Learning:

Neuro-Symbolic PDE Solver

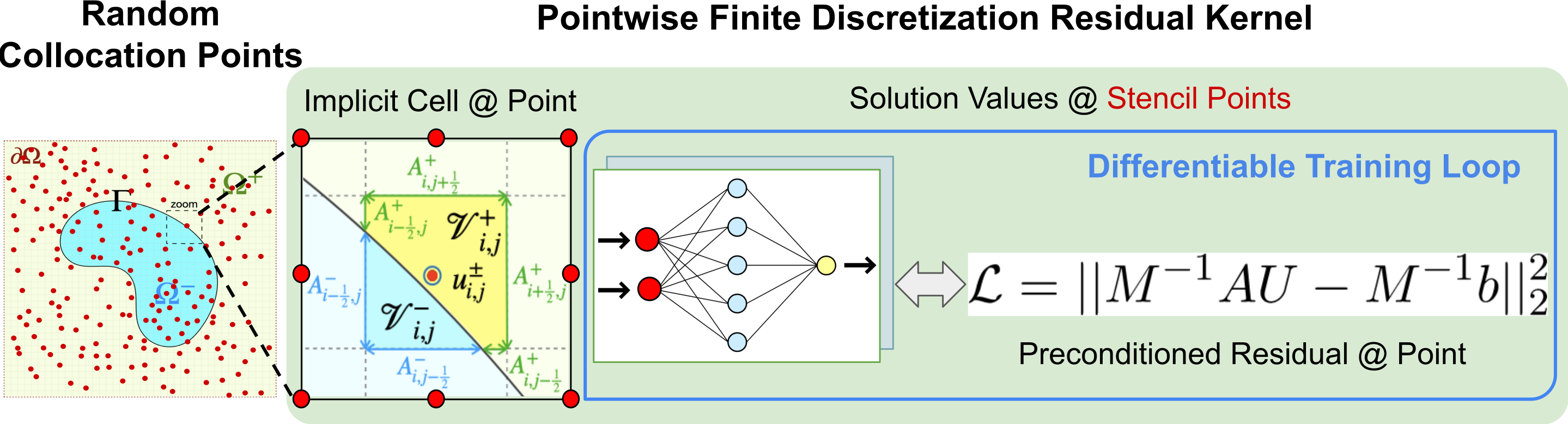
We present a scalable strategy for development of mesh-free hybrid neuro-symbolic partial differential equation solvers based on existing mesh-based numerical discretization methods. Particularly, this strategy can be used to efficiently train neural network surrogate models for the solution functions and operators of partial differential equations while retaining the accuracy and convergence properties of the state-of-the-art numerical solvers. The presented neural bootstrapping method (hereby dubbed NBM) is based on evaluation of the finite discretization residuals of the PDE system obtained on implicit Cartesian cells centered on a set of random collocation points with respect to trainable parameters of the neural network. We apply NBM to the important class of elliptic problems with jump conditions across irregular interfaces in three spatial dimensions. We show the method is convergent such that model accuracy improves by increasing number of collocation points in the domain. The algorithms presented here are implemented and released in a software package named JAX-DIPS, standing for differentiable interfacial PDE solver. JAX-DIPS is purely developed in JAX, offering end-to-end differentiability from mesh generation to the higher level discretization abstractions, geometric integrations, and interpolations, thus facilitating research into use of differentiable algorithms for developing hybrid PDE solvers.

Cell's Photo

- HPC Simulations:

Computational Biophysics: Cell Aggregate Electroporation

  • An efficient framework for direct simulations of the mesoscale cell aggregates (tissue scale) is proposed.
  • The Electropermeabilization model is simulated on a Voronoi mesh in a parallel environment that is developed in the context of the level-set method.
  • For the first time, direct simulations of the multi-scale electroporation phenomena such as shadowing effect, permeabilization saturation, tissue-scale homogenization, and memory effects have become possible.
  • The proposed framework surpasses the existing implementations by enabling simulations of arbitrarily large tissues given enough number of processors being available.

Cell's Photo

Computational Materials Science: Epitaxial Growth

  • An efficient framework for simulating various features of epitaxial growth at the mesoscale is proposed.
  • The island dynamics model (IDM) is simulated on a forest of quadtree grids in a parallel environment that is developed in the context of the level-set method.
  • Both Dirichlet and Robin boundary conditions for the adatom density at the island boundaries are implemented.
  • The proposed framework surpasses the existing implementations of the IDM in terms of efficiency by several orders of magnitudes without loss of accuracy.

Atom's Photo

Computational Astrophysics: Formation and Evolution of Dwarf Galaxies

Galaxy clusters contain a large population of low-mass dwarf elliptical galaxies whose exact origin is unclear: their colours, structural properties and kinematics differ substantially from those of dwarf irregulars in the field. We use the Illustris cosmological simulation to study differences in the assembly histories of dwarf galaxies (3 × 10^8 < M*/M⊙ < 10^10) according to their environment. We find that cluster dwarfs achieve their maximum total and stellar mass on average ∼8 and ∼4.5 Gyr ago (or redshifts z=1.0 and 0.4, respectively), around the time of infall into the clusters. In contrast, field dwarfs not subjected to environmental stripping reach their maximum mass at z=0. These different assembly trajectories naturally produce a colour bimodality, with blue isolated dwarfs and redder cluster dwarfs exhibiting negligible star formation today. The cessation of star formation happens over median times 3.5–5 Gyr depending on stellar mass, and shows a large scatter (∼1–8 Gyr), with the lower values associated with starburst events that occur at infall through the virial radius or pericentric passages. We argue that such starbursts together with the early assembly of cluster dwarfs can provide a natural explanation for the higher specific frequency of globular clusters (GCs) in cluster dwarfs, as found observationally. We present a simple model for the formation and stripping of GCs that supports this interpretation. The origin of dwarf ellipticals in clusters is, therefore, consistent with an environmentally driven evolution of field dwarf irregulars. However, the z=0 field analogues of cluster dwarf progenitors have today stellar masses a factor of ∼3 larger – a difference arising from the early truncation of star formation in cluster dwarfs.

Galaxy's Photo